In the area of kinematics of spatial mechanisms, we have focused our attention on:
- calibration of industrial robots, and
- singularity analysis of non-redundant mechanisms.
An optimization methodology has been developed in response to potential high costs associated with industrial-robot calibration. The objective of minimizing residual error after calibration is combined with the objective of minimizing the cost of calibration into a multi-criterion non-linear programming problem.
The main difficulty in carrying out such an optimization process is to directly measure the residual error of the robot for every set of variables evaluated by the algorithm. One solution is to use a response-surface methodology can be used to obtain a second-order polynomial response-surface representation of the observed (via experiments or simulations) residual-error data.
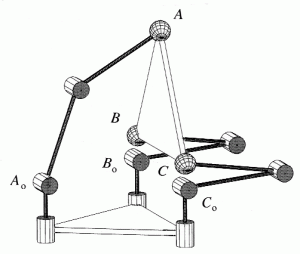
In regard to the second area of research, a general theory for the singularity analysis of non-redundant mechanisms has been developed. On the basis of a general velocity equation, derived as a necessary and sufficient condition for the feasibility of the instantaneous motion of a mechanism, a new general definition of singularity is proposed.
The velocity equation explicitly includes the passive-joint velocities in addition to all input and output velocities of the mechanism. A configuration is regarded as singular when either the forward or the inverse kinematics problem does not have a general solution.
Six types of singularities, reflecting different possibilities for the occurrence of indeterminacy of the instantaneous kinematics, were defined.